
Book: Complexity: A Guided Tour
Author: Melanie Mitchell
Genre: Science
Rating: ★★★★
Buy now on Amazon
Review: If we were to describe Complexity: A Guided Tour like a wine connoisseur, its aroma would be complex, with a hint of regret – regret that you ever thought reading this book would be a breeze! The flavour is jam-packed with concepts that can be tough to digest, like trying to swallow a whole grapefruit without wincing. The mouthfeel is heavy, intellectual, and bone dry – a true challenge for even the most seasoned readers. Despite its difficulty, this book is worth the effort. Stick with it, and you’ll come away with a deeper understanding of the interconnected systems that shape our world.
Chapter 1: What is Complexity?
This chapter introduces the concept of complex systems, composed of many individual components that collectively give rise to complex and unpredictable behaviour. It discusses several examples of complex systems, including ant colonies, the immune system, economies, and the World Wide Web. It highlights their common properties, such as collective behaviour, signalling and information processing, and adaptation. The author also provides two possible definitions of a complex system and explores how complexity can be measured. It ends by noting that there is no agreed-upon quantitative definition of complexity, but that the struggle to define the central terms is a crucial part of forming a new science.
Two possible definitions of a complex system are proposed:
- The first definition is based on the system’s behaviour: a complex system is a system that exhibits behaviours that cannot be understood by simply studying its parts.
- The second definition is based on the system’s structure: a complex system is a system made up of many interacting parts, where the interactions between the parts give rise to collective behaviours that cannot be predicted from the properties of the individual parts.
Both definitions highlight the idea that complexity arises from the interactions and relationships between the components of a system, rather than from the properties of the components themselves.
How complexity can be measured?
- Number of parts or elements: Complexity can be related to the number of parts or elements that make up a system. Generally, the more parts or elements a system has, the more complex it is likely to be.
- Number of interactions: Complexity can also be related to the number of interactions between parts or elements in a system. The more interactions there are, the more complex the system is likely to be.
- Emergent behaviour: Complex systems often exhibit emergent behaviour, which is behaviour that arises from the interactions between the parts or elements of the system. Measuring emergent behaviour can be challenging, but it is a critical aspect of measuring complexity.
- Information content: Another way to measure complexity is by looking at the amount of information that is needed to describe or understand the system. Complex systems may require a large amount of data to be understood fully.
Chapter 2: Dynamics, Chaos, and Prediction
Chapter 2 introduces the basic concepts of chaos theory and the dynamical systems that exhibit it. Chaos theory can be summarised as follows:
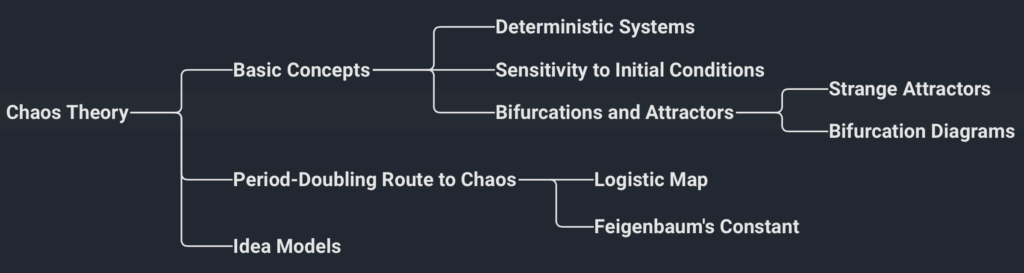
- Deterministic systems: Chaos theory studies the behaviour of deterministic systems, which are systems that are completely determined by their initial conditions and the laws governing their evolution over time.
- Sensitivity to initial conditions: Small changes in the initial conditions of a chaotic system can lead to drastically different outcomes over time. This is known as the butterfly effect, where the flap of a butterfly’s wings in Brazil can cause a tornado in Texas.
- Bifurcations and attractors: As the parameters of a chaotic system are changed, the system can undergo a bifurcation, which leads to a sudden change in its behaviour. The system can also settle into an attractor, which is a set of states that the system tends to move toward over time.
- Period-doubling route to chaos: This is a universal feature of many chaotic systems, whereas the parameters of the system are changed, the system undergoes a sequence of bifurcations, leading to the appearance of periodic orbits of increasing period, until it eventually enters a state of chaos.
- The logistic map is a mathematical function that is often used as a simple model system to study chaos and its properties. It is a non-linear differential equation that describes how the population of a species might grow under certain conditions. By iterating the function with different values of a parameter, researchers can explore how the system’s behaviour changes and how it exhibits different features of chaos theory, such as bifurcations, attractors, and the period-doubling route to chaos.
- Idea models: Chaos theory often makes use of idea models, which are simple models that capture the essential features of complex systems. These models can be studied mathematically or using computers to gain insight into the behaviour of real-world systems.
Chapter 3: Information
Chapter 3 introduces the concepts of information and entropy and how they relate to the second law of thermodynamics. It begins by discussing the origin of the second law and how it implies that heat can only flow from hot to cold and that systems will always tend towards greater disorder or entropy.
It then moves on to explain the difference between microstates and macrostates, which are used to describe the possible configurations of a system’s particles. Microstates are the specific positions and velocities of all the particles, while macrostates are the collection of all possible microstates that lead to the same overall configuration.
It also describes Boltzmann’s entropy, which is defined in terms of the number of microstates corresponding to a given macrostate, and how it relates to the second law.
Then it shifts to discussing Claude Shannon’s information theory, which is based on Boltzmann’s ideas about entropy. Shannon’s work is focused on the problem of transmitting information over a noisy channel, such as a telephone wire, and how to maximize the transmission rate while minimising errors. Shannon defines information in terms of the number of possible messages that can be sent by a source, and his definition of information content is similar to Boltzmann’s entropy.
……..I gave up reading chapters 4 to 19 (for now)
Buy now on Amazon
◃ Back
